The Busy Beaver Problem

Busy Beaver puts another one on the Turing Machine’s tape.
(image from a book “the new turing omnibus“)

The busy beaver problem is a fun theoretical computer science problem to know. Intuitively, the problem is to find the smallest program that outputs as many data as possible and eventually halts. More formally it goes like this — given an n-state Turing Machine with a two symbol alphabet {0, 1}, what is the maximum number of 1s that the machine may print on an initially blank tape (0-filled) before halting?

It turns out that this problem can’t be solved. For a small number of states it can be reasoned about, but it can’t be solved in general. Theorists call such problems non-computable.

Currently people have managed to solve it for n=1,2,3,4 (for Turing Machines with 1, 2, 3 and 4 states) by reasoning about and running all the possible Turing Machines, but for n ≥ 5 this task has currently been impossible. While most likely it will be solved for n=5, theorists doubt that it shall ever be computed for n=6.

Let’s denote the number of 1s that the busy beaver puts on a tape after halting as S(n) and call it the busy beaver function (this is the solution to the busy beaver problem). The busy beaver function is also interesting — it grows faster than any computable function. It grows like this:

• S(1) = 1
• S(2) = 4
• S(3) = 6
• S(4) = 13
• S(5) ≥ 4098 (the exact result has not yet been found)
• S(6) ≥ 4.6 · 10¹⁴³⁹ (the exact result shall never be known)

If we were to use one atom for each 1 that the busy beaver puts on the tape, at n=6 we would have filled the whole universe! That’s how fast the busy beaver function is growing.

I decided to play with the busy beaver myself to verify the known results for n ≤ 5. I implemented a Turing Machine in Python, which turned out to be too slow, so I reimplemented it in C++ (source code of both implementations below).

I also wrote a visualization tool in Perl that shows how the Turing Machine’s tape changes from the start to the finish (source code also below).

I used the following best known Turing Machines. Their tapes are initially filled with 0’s, their starting state is ” a ” and halting state is ” h “. The notation ” a0 -> b1l ” means “if we are in the state “a” and the current symbol on the tape is “0″ then put a “1″ in that cell, switch to state “b” and move to left “l”. This process repeats until the machine ends up in the halting state.

Turing Machine for 1-state Busy Beaver:

a0 -> h1r

Turing Machine for 2-state Busy Beaver:

a0 -> b1r    a1 -> b1l
b0 -> a1l    b1 -> h1r

Here is how the trace of tape changes look like for the 2-state busy beaver:

Tape changes for 2 state busy beaver.

Turing Machine for 3-state Busy Beaver:

a0 -> b1r    a1 -> h1r
b0 -> c0r    b1 -> b1r
c0 -> c1l    c1 -> a1l

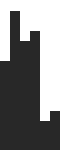
Tape changes for 3 state busy beaver.

Turing Machine for 4-state Busy Beaver:

a0 -> b1r    a1 -> b1l
b0 -> a1l    b1 -> c0l
c0 -> h1r    c1 -> d1l
d0 -> d1r    d1 -> a0r

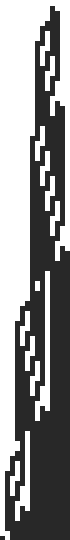
Tape changes for 4 state busy beaver.

Turing Machine for 5-state Busy Beaver:

a0 -> b1l    a1 -> a1l
b0 -> c1r    b1 -> b1r
c0 -> a1l    c1 -> d1r
d0 -> a1l    d1 -> e1r
e0 -> h1r    e1 -> c0r

This image is huge (6146 x 14293 pixels, but only 110KB in size). Click for full size.

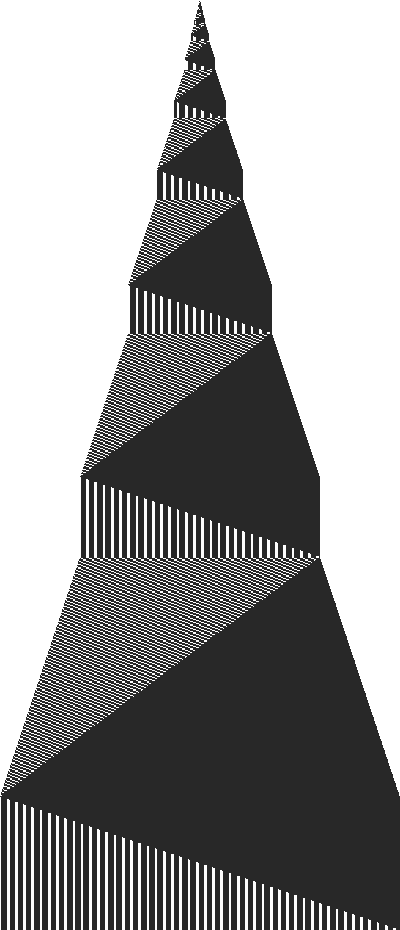
Tape changes for 5 state busy beaver.

Turing Machine for 6 state Busy Beaver:

a0 -> b1r    a1 -> e0l
b0 -> c1l    b1 -> a0r
c0 -> d1l    c1 -> c0r
d0 -> e1l    d1 -> f0l
e0 -> a1l    e1 -> c1l
f0 -> e1l    f1 -> h1r

Here is my Python program to simulate all these Turing Machines. But as I said, it turned out to be too slow. For the 5 state Busy Beaver it took 5 minutes to generate the currently best known solution.

Download: busy_beaver.py (380)

#!/usr/bin/python
#
# Turing Machine simulator for Busy Beaver problem.
# Version 1.0
#

import sys

class Error(Exception):
    pass

class TuringMachine(object):
    def __init__(self, program, start, halt, init):
        self.program = program
        self.start = start
        self.halt = halt
        self.init = init
        self.tape = [self.init]
        self.pos = 0
        self.state = self.start
        self.set_tape_callback(None)
        self.tape_changed = 1
        self.movez = 0

    def run(self):
        tape_callback = self.get_tape_callback()
        while self.state != self.halt:
            if tape_callback:
                tape_callback(self.tape, self.tape_changed)

            lhs = self.get_lhs()
            rhs = self.get_rhs(lhs)

            new_state, new_symbol, move = rhs

            old_symbol = lhs[1]
            self.update_tape(old_symbol, new_symbol)
            self.update_state(new_state)
            self.move_head(move)

        if tape_callback:
            tape_callback(self.tape, self.tape_changed)

    def set_tape_callback(self, fn):
        self.tape_callback = fn

    def get_tape_callback(self):
        return self.tape_callback

    property(get_tape_callback, set_tape_callback)

    @property
    def moves(self):
        return self.movez

    def update_tape(self, old_symbol, new_symbol):
        if old_symbol != new_symbol:
            self.tape[self.pos] = new_symbol
            self.tape_changed += 1
        else:
            self.tape_changed = 0

    def update_state(self, state):
        self.state = state

    def get_lhs(self):
        under_cursor = self.tape[self.pos]
        lhs = self.state + under_cursor
        return lhs

    def get_rhs(self, lhs):
        if lhs not in self.program:
            raise Error('Could not find transition for state "%s".' % lhs)
        return self.program[lhs]

    def move_head(self, move):
        if move == 'l':
            self.pos -= 1
        elif move == 'r':
            self.pos += 1
        else:
            raise Error('Unknown move "%s". It can only be left or right.' % move)

        if self.pos < 0:
            self.tape.insert(0, self.init)
            self.pos = 0
        if self.pos >= len(self.tape):
            self.tape.append(self.init)

        self.movez += 1

beaver_programs = [
    { },

    {'a0': 'h1r' },

    {'a0': 'b1r', 'a1': 'b1l',
     'b0': 'a1l', 'b1': 'h1r'},

    {'a0': 'b1r', 'a1': 'h1r',
     'b0': 'c0r', 'b1': 'b1r',
     'c0': 'c1l', 'c1': 'a1l'},

    {'a0': 'b1r', 'a1': 'b1l',
     'b0': 'a1l', 'b1': 'c0l',
     'c0': 'h1r', 'c1': 'd1l',
     'd0': 'd1r', 'd1': 'a0r'},

    {'a0': 'b1l', 'a1': 'a1l',
     'b0': 'c1r', 'b1': 'b1r',
     'c0': 'a1l', 'c1': 'd1r',
     'd0': 'a1l', 'd1': 'e1r',
     'e0': 'h1r', 'e1': 'c0r'},

    {'a0': 'b1r', 'a1': 'e0l',
     'b0': 'c1l', 'b1': 'a0r',
     'c0': 'd1l', 'c1': 'c0r',
     'd0': 'e1l', 'd1': 'f0l',
     'e0': 'a1l', 'e1': 'c1l',
     'f0': 'e1l', 'f1': 'h1r'}
]

def busy_beaver(n):
    def tape_callback(tape, tape_changed):
        if tape_changed:
            print ''.join(tape)

    program = beaver_programs[n]

    print "Running Busy Beaver with %d states." % n
    tm = TuringMachine(program, 'a', 'h', '0')
    tm.set_tape_callback(tape_callback)
    tm.run()
    print "Busy beaver finished in %d steps." % tm.moves

def usage():
    print "Usage: %s [1|2|3|4|5|6]" % sys.argv[0]
    print "Runs Busy Beaver problem for 1 or 2 or 3 or 4 or 5 or 6 states."
    sys.exit(1)

if __name__ == "__main__":
    if len(sys.argv[1:]) < 1:
        usage()

    n = int(sys.argv[1])

    if n < 1 or n > 6:
        print "n must be between 1 and 6 inclusive"
        print
        usage()

    busy_beaver(n)

I rewrote the Turing Machine simulator in C++ and the speedup was huge. Now it took 14 seconds to execute the same Busy Beaver 5.

Download: busy_beaver.cpp (382)

/*
** Turing Machine simulator for Busy Beaver problem.
** Version 1.0
*/

#include <cstdlib>
#include <iostream>
#include <utility>
#include <vector>
#include <string>
#include <map>

using namespace std;

typedef vector<char> Tape;
typedef map<string, string> Program;

class TuringMachine {
private:
    Tape tape;
    Program program;
    char start, halt, init, state;
    bool tape_changed;
    int moves;
    int pos;
public:
    TuringMachine(Program program, char start, char halt, char init):
        tape(1, init), program(program), start(start), halt(halt),
        init(init), state(start), moves(0), tape_changed(1), pos(0)
    { }

    void run() {
        while (state != halt) {
            print_tape();
            string lhs = get_lhs();
            string rhs = get_rhs(lhs);

            char new_state = rhs[0];
            char new_symbol = rhs[1];
            char move = rhs[2];

            char old_symbol = lhs[1];
            update_tape(old_symbol, new_symbol);
            update_state(new_state);
            move_head(move);
        }
        print_tape();
    }

    int get_moves() {
        return moves;
    }

private:
    inline void print_tape() {
        if (tape_changed) {
            for (int i=0; i<tape.size(); i++)
                cout << tape[i];
            cout << endl;
        }
    }

    inline string get_lhs() {
        char sp[3] = {0};
        sp[0] = state;
        sp[1] = tape[pos];
        return string(sp);
    }

    inline string get_rhs(string &lhs) {
        return program[lhs];
    }

    inline void update_tape(char old_symbol, char new_symbol) {
        if (old_symbol != new_symbol) {
            tape[pos] = new_symbol;
            tape_changed++;
        }
        else {
            tape_changed = 0;
        }
    }

    inline void update_state(char new_state) {
        state = new_state;
    }

    inline void move_head(char move) {
        if (move == 'l')
            pos -= 1;
        else if (move == 'r')
            pos += 1;
        else
            throw string("unknown state");

        if (pos < 0) {
            tape.insert(tape.begin(), init);
            pos = 0;
        }
        if (pos >= tape.size()) {
            tape.push_back(init);
        }
        moves++;
    }

};

vector<Program> busy_beavers;

void init_bb6()
{
    Program bb6;
    bb6.insert(make_pair("a0", "b1r"));
    bb6.insert(make_pair("b0", "c1l"));
    bb6.insert(make_pair("c0", "d1l"));
    bb6.insert(make_pair("d0", "e1l"));
    bb6.insert(make_pair("e0", "a1l"));
    bb6.insert(make_pair("f0", "e1l"));

    bb6.insert(make_pair("a1", "e0l"));
    bb6.insert(make_pair("b1", "a0r"));
    bb6.insert(make_pair("c1", "c0r"));
    bb6.insert(make_pair("d1", "f0l"));
    bb6.insert(make_pair("e1", "c1l"));
    bb6.insert(make_pair("f1", "h1r"));

    busy_beavers.push_back(bb6);
}

void init_bb5()
{
    Program bb5;
    bb5.insert(make_pair("a0", "b1l"));
    bb5.insert(make_pair("b0", "c1r"));
    bb5.insert(make_pair("c0", "a1l"));
    bb5.insert(make_pair("d0", "a1l"));
    bb5.insert(make_pair("e0", "h1r"));

    bb5.insert(make_pair("a1", "a1l"));
    bb5.insert(make_pair("b1", "b1r"));
    bb5.insert(make_pair("c1", "d1r"));
    bb5.insert(make_pair("d1", "e1r"));
    bb5.insert(make_pair("e1", "c0r"));

    busy_beavers.push_back(bb5);
}

void init_bb4()
{
    Program bb4;
    bb4.insert(make_pair("a0", "b1r"));
    bb4.insert(make_pair("b0", "a1l"));
    bb4.insert(make_pair("c0", "h1r"));
    bb4.insert(make_pair("d0", "d1r"));

    bb4.insert(make_pair("a1", "b1l"));
    bb4.insert(make_pair("b1", "c0l"));
    bb4.insert(make_pair("c1", "d1l"));
    bb4.insert(make_pair("d1", "a0r"));

    busy_beavers.push_back(bb4);

}

void init_bb3()
{
    Program bb3;
    bb3.insert(make_pair("a0", "b1r"));
    bb3.insert(make_pair("b0", "c0r"));
    bb3.insert(make_pair("c0", "c1l"));

    bb3.insert(make_pair("a1", "h1r"));
    bb3.insert(make_pair("b1", "b1r"));
    bb3.insert(make_pair("c1", "a1l"));

    busy_beavers.push_back(bb3);
}

void init_bb2()
{
    Program bb2;
    bb2.insert(make_pair("a0", "b1r"));
    bb2.insert(make_pair("b0", "a1l"));

    bb2.insert(make_pair("a1", "b1l"));
    bb2.insert(make_pair("b1", "h1r"));

    busy_beavers.push_back(bb2);
}

void init_bb1()
{
    Program bb1;
    bb1.insert(make_pair("a0", "h1r"));

    busy_beavers.push_back(bb1);
}

void init_busy_beavers()
{
    busy_beavers.push_back(Program());
    init_bb1();
    init_bb2();
    init_bb3();
    init_bb4();
    init_bb5();
    init_bb6();
}

void busy_beaver(int n)
{
    cout << "Running Busy Beaver with " << n << " states." << endl;
    TuringMachine tm(busy_beavers[n], 'a', 'h', '0');
    tm.run();
    cout << "Busy Beaver finished in " << tm.get_moves() << " steps." << endl;
}

void usage(const char *prog)
{
    cout << "Usage: " << prog << " [1|2|3|4|5|6]\n";
    cout << "Runs Busy Beaver problem for 1 or 2 or 3 or 4 or 5 or 6 states." << endl;
    exit(1);
}

int main(int argc, char **argv)
{
    if (argc < 2) {
        usage(argv[0]);
    }

    int n = atoi(argv[1]);
    if (n < 1 || n > 6) {
        cout << "n must be between 1 and 6 inclusive!\n";
        cout << "\n";
        usage(argv[0]);
    }

    init_busy_beavers();
    busy_beaver(n);
}

And I also wrote a Perl program that uses the GD library to draw the tape changes on Turing Machines.

Download: draw_turing_machine.perl (324)

#!/usr/bin/perl
#
# Given output from busy_beaver.py or busy_beaver.cpp,
# draws the turing machine tape changes.
#

use warnings;
use strict;
use GD;

$|++;

my $input_file = shift or die 'Usage: $0 <file with TM state transitions>';
my $cell_size = shift || 4;
my $im_file = "$input_file.png";

sub line_count {
    my $count = 0;
    open my $fh, '<', shift or die $!;
    $count += tr/\n/\n/ while sysread($fh, $_, 2**20);
    return $count;
}

sub get_last_line {
    my $file = shift;
    my $last_line = `tail -1 $file`;
    chomp $last_line;
    return $last_line;
}

my $nr_lines = line_count $input_file;
my $last_line = get_last_line $input_file;
my $last_width = length($last_line);

my ($width, $height) = ($cell_size*$last_width, $cell_size*$nr_lines);

my $im = GD::Image->new($width, $height);
my $white = $im->colorAllocate(255,255,255);
my $dark = $im->colorAllocate(40, 40, 40);

my ($x, $y) = (0, $height-$cell_size);

print "Starting to draw the image. Total states: $nr_lines.\n";
print "It will be $width x $height pizels in size.\n";

my $prev_line;
my ($pad_left, $pad_right) = (0, 0);

sub pad {
    my ($line, $left, $right) = @_;
    return '0'x$left . $line . '0'x$right;
}

open my $fh, "-|", "/usr/bin/tac $input_file" or die $!;
while (<$fh>) {
    chomp;
    print "." if $. % 10 == 0;
    print "($.)" if $. % 500 == 0;

    $prev_line = $_ unless defined $prev_line;

    my $new_line;
    if (length $_ != length $prev_line) {
        if ($prev_line =~ /0$/) {
            $pad_right++;
        }
        elsif ($prev_line =~ /^0/) {
            $pad_left++;
        }
        else {
            die "unexpected data at $. in file $input_file";
        }
    }
    $new_line = pad($_, $pad_left, $pad_right);
    $prev_line = $_;

    my @cells = split //, $new_line;
    for my $cell (@cells) {
        $im->filledRectangle($x, $y, $x + $cell_size, $y + $cell_size,
                $cell ? $dark : $white);
        $x += $cell_size;
    }
    $y -= $cell_size;
    $x = 0;

}

print "\n";

{
    open my $fh, ">", $im_file or die $!;
    print $fh $im->png;
    close $fh;
}

print "Done. Image saved to $im_file.\n";

You can play with these programs yourself. Here is how. Run “busy_beaver.py <n>” with n=1,2,3,4,5,6. This will run the n-state busy beaver Turing Machine. The output will be the tape changes. Then use “draw_turing_machine.pl” to visualize the tape changes.

For example:

$ busy_beaver.py 4 > bb4
$ draw_turing_machine.pl bb4

There are variations of this problem. For example, the busiest beaver with 3 and more symbols. See “The Busy Beaver Competition” for these. The historical development is also interesting — see The Busy Beaver Historical Survey for more info.

I first learned about the Busy Beaver problem from a book called “The New Turing Omnibus.” It contains 66 different essays on various computer science subjects such as algorithms, turing machines, grammars, computability, randomness, and other fun topics. These essays are written in an accessible style that even a high school student can understand them. Each essay doesn’t take more than 10 minutes to read. I recommend this book. Get it here: